What is my scheduling objective? Lower bounds on the total project duration
Submitted by Mario Vanhoucke on Thu, 01/19/2012 - 15:48
Minimizing the total duration of a resource-constrained project is often a generally accepted project scheduling objective (see “What is my scheduling objective? Minimizing the project lead time”). However, optimizing a scheduling objective within the presence of limited renewable resources often requires software algorithms. In this article, three lower bound calculations will be discussed, as follows:
- Critical path lower bound: ignores the resource constraints and only looks at the project network
- Resource based lower bound: ignores the project network and only looks at the the resource constraints
- Critical sequence lower bound: combination of the two previous bounds by looking at both the project network and resource constraints
Figure 1 displays a project network with 11 activities and finish-start precedence relations. Each number above the node denotes the estimated duration of the activity while the number below the node is used to refer to the resource demand. The maximum availability of the resource is equal to 5 units (e.g. people). More information on resource demand and availability is given in “Linking resources to activities: Resource availability and resource demand”.
?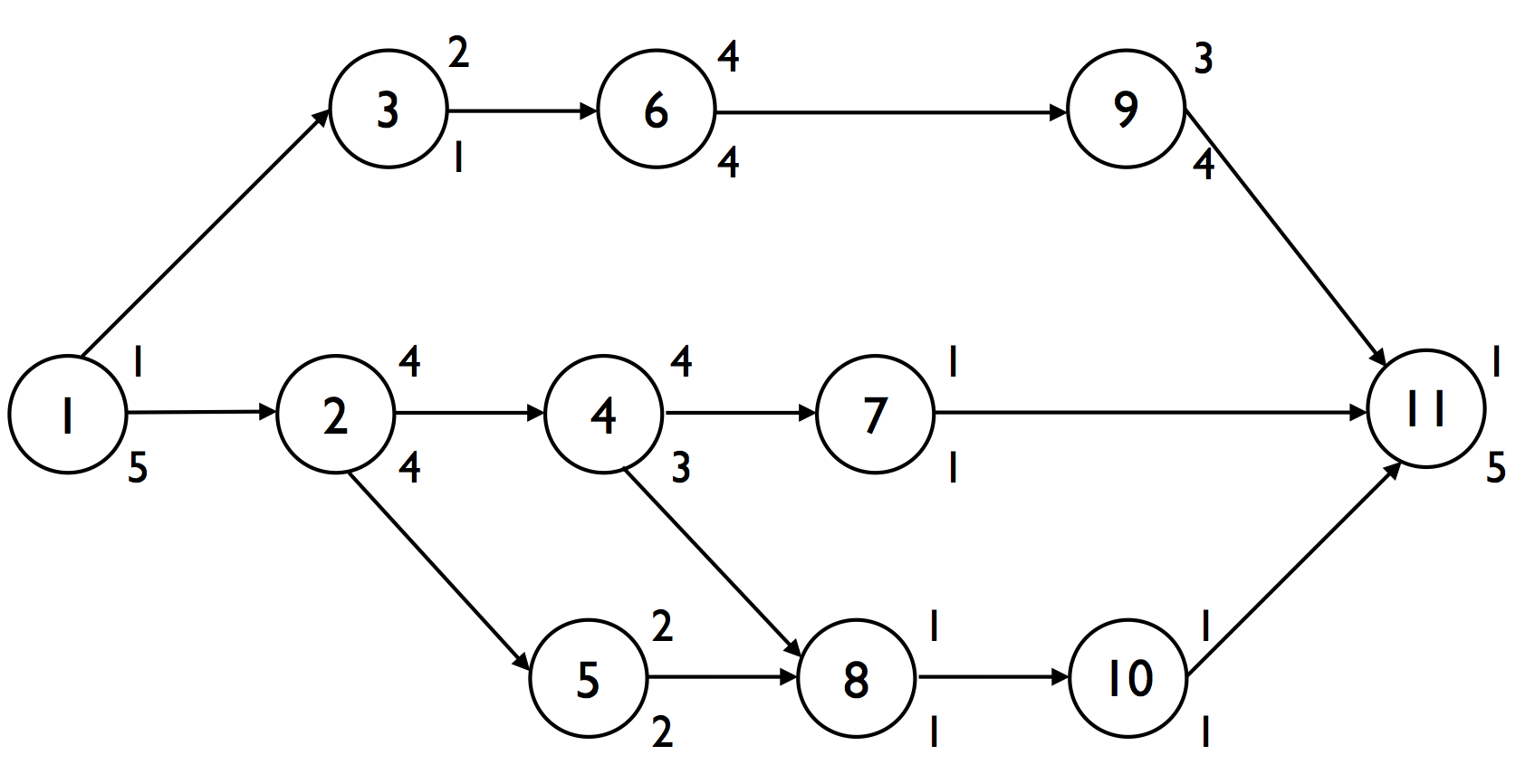

Figure 1: Project network and activity data
Critical path lower bound (CPLB)
In the critical path calculations proposed by the PERT/CPM scheduling approach, projects are not subject to limited renewable resources, and hence, the construction of a baseline schedule boils down to sequencing all activities according to their precedence relations. The minimal duration of the project is determined by the length of the critical path, which is a sequence of activities in the project network. The critical path of the project network of figure 1 is equal to 1 - 2 - 4 - 8 - 10 - 11 with a total length equal to 12 time units.
Obviously, when the limited availability of the renewable resources is taken into account, the minimal project duration will probably increase (due to the presence of resource conflicts), or remain unchanged (see “The critical path or the critical chain?: The difference caused by resources”). Consequently, the critical path duration of 12 time units is a lower bound on the real project duration of the resource-constrained project of figure 1.
Resource based lower bound (RBLB)
While the critical path lower bound only takes the precedence relations into account and ignores the presence of limited renewable resources, the resource based lower bound takes an inverse approach. It looks at the total use of resources for all project activities and ignores the precedence relations between the activities. The lower bound is equal to the sum of the work content (= activity duration multiplied by its resource requirement) of all activities divided by the availability of resources, as follows:
- Sum of work content = 1 * 5 + 4 * 4 + 2 * 1 + 4 * 3 + 2 * 2 + 4 * 4 + 1 * 1 + 1 * 1 + 3 * 4 + 1 * 1 + 1 * 5 = 75
- Lower bound = 75 / 5 = 15
In the example, the resource based lower bound value is bigger than than the critical path lower bound value, but this is obviously not always the case since they both have a completely different calculation approach. The highest lower bound is retained as the strongest lower bound, and hence, at this point it can be concluded that a resource feasible schedule must have a duration of minimum 15 time units, or probably higher.
Critical sequence lower bound (CSLB)
While the critical path lower bound only takes the precedence relations into account but ignores the resources, and the resource based lower bound does exactly the opposite, the critical sequence lower bound considers both the precedence and the resource constraints in a two step approach:
- Step 1: Consider a critical path in the network and set the CSLB = CPLB
-
Step 2: Do for each noncritical activity i
- Determine the earliest start ESi and latest finish LFi
- Determine how many time periods ei this activity can be scheduled consecutively in parallel with the activities on the critical path (between ESi and LFi)
- if(ei < di) then set ?i = di - ei else ?i = 0
- Step 3: CSLB = CPLB + maximum of all ?i values
with
?i: Increase in the critical path length to add activity i in the schedule without generating a resource conflict
ESi: Earliest start of activity i
LFi: Latest finish of activity i
ei: Number of periods between ESi and LFi with the remaining resource availability ≥ resource demand for activity i
di: Duration of activity i
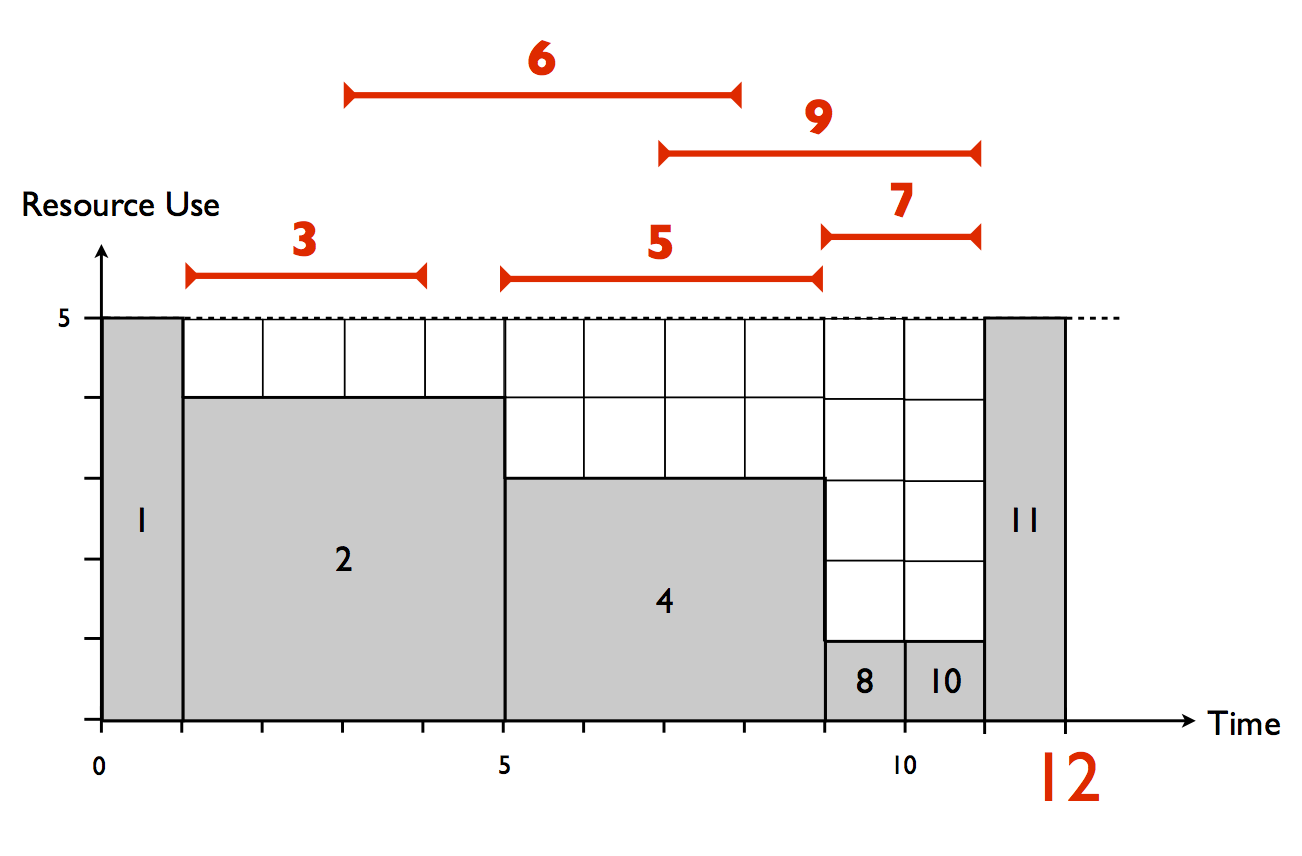
Figure 2 displays the critical path activities with a total length of 12 time units and the earliest start and latest finish of all noncritical activities. For each noncritical activity, the difference between its earliest start and its latest finish is indicated by the arcs above the schedule.
?

Figure 2. Schedule with the critical activities and their resource use
Table 1 displays the information about the noncritical activities needed to calculate the critical sequence lower bound. Consider, as an example, activity 9 which has four periods between its earliest start and latest finish, of which only 2 time periods have enough resources (4 units). Consequently, the e9 value is equal to 2 time units. Since e9 < d9, the ?9 parameter is set to 1 to express that the critical path length of 12 must be increased by one time period in order to add activity 9 to the schedule without generating a resource conflict. Activity 6, for example, has no periods between its earliest start and latest finish with enough resources (the activity needs 4 units and maximum 2 are available in figure 2) and hence, e6 = 0 and ?6 = 4 - 0 = 4. Doing these calculations for each activity and taking the maximum of all ?i values leads to the critical sequence lower bound equal to 12 + 4 = 16 time units. A stepwise calculation of all values in table 2 is illustrated in “Animation: Three lower bounds”.
Table 1: Parameter calculations for all noncritical activities to calculate the CSLB
| Activity i | di | ESi | LFi | ei | ?i |
| 3 | 2 | 1 | 4 | 3 | 0 |
| 5 | 2 | 5 | 9 | 4 | 0 |
| 6 | 4 | 3 | 8 | 0 | 4 |
| 7 | 1 | 9 | 11 | 2 | 0 |
| 9 | 3 | 7 | 11 | 2 | 1 |
Conclusion
As a general conclusion, the maximum of all lower bounds is equal to max{12, 15, 16} = 16 and hence, any resource feasible schedule must have a total project duration which is equal to 16 time periods, or possibly larger. It is worth noting the the minimal project duration is equal to 17 time units, which is one time unit larger than the best lower bound found in this article. It is up to the reader to construct such a resource feasible schedule using techniques as described in “Optimizing regular scheduling objectives: Priority rule based scheduling”. Although lower bound calculations do not lead to a resource feasible schedule, they might provide the user with information on the solution quality of a scheduling tool, as illustrated in “Heuristic project scheduling: Validating the quality of a project schedule”.
© OR-AS. PM Knowledge Center is made by OR-AS bvba | Contact us at info@or-as.be | Visit us at www.or-as.be | Follow us at @ORASTalks


