What is my scheduling objective? Maximizing the net present value
When finishing this article, you can take a short "Test Yourself" quiz, to ensure you fully understood this topic.
Resource-constrained project scheduling involves the construction of an activity timetable, i.e. the determination of a start and finish time for each project activity, respecting the precedence relations and the limited availability of the renewable resources, while optimizing a predefined scheduling objective (see “Resource constrained project scheduling: What is my scheduling objective?”). In this article, the scheduling objective is assumed to be the maximization of the net present value of the project.
Figure 1 displays a project network with 11 activities and finish-start precedence relations between them. Each number above the node denotes the estimated duration of the activity while the numbers below the node are used to refer to the net cash flows (payments – receipts) and resource demand. Remark that these cash flows are represented as a terminal value, realized at the end of each activity. It is assumed that the availability of the resource is restricted to six units for all periods of the project. The right part of the picture displays an earliest start schedule respecting the precedence relations of the project. Each activity is represented by a rectangle with the horizontal length the activity duration and the vertical height the renewable resource requirement/demand. The earliest start schedule shows a resource conflict between period 8 and 13 since the total use of the renewable resource by activities 3, 4, 5, 6 and 7 exceeds its limited availability of 6. In order to solve this resource conflict, activities need to be shifted further in time to time periods where resources are still available (see “Linking resources to activities: Resource availability and resource demand”).
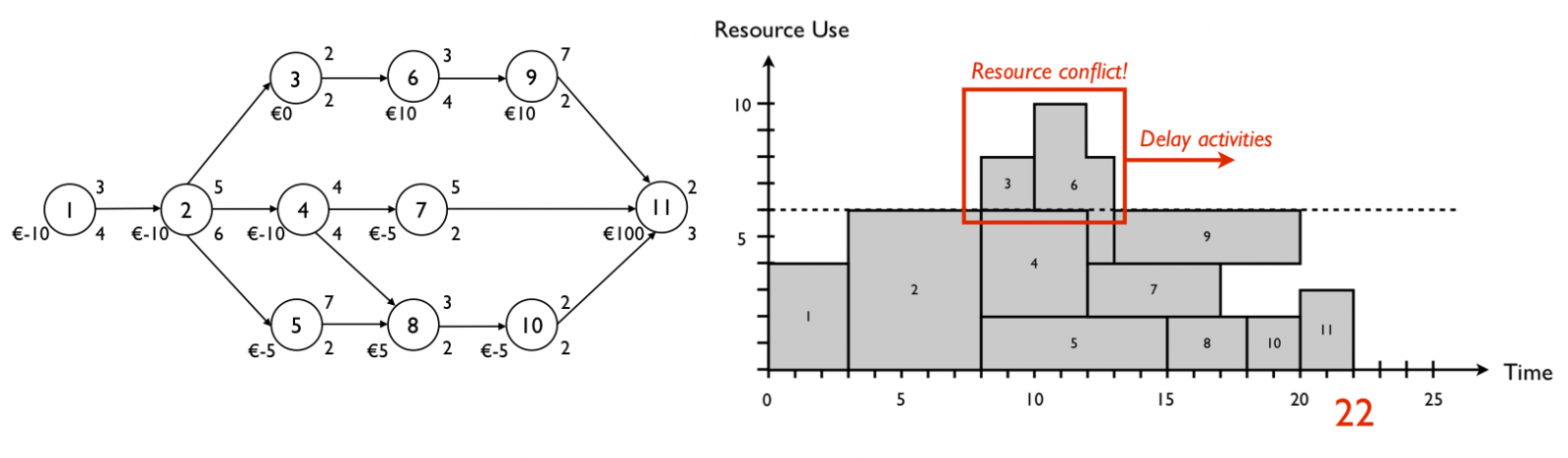
Figure 1: Project network with activity data and the resource profile of the earliest start schedule
The net present value
Any project involves large financial implications. Costs (cash outflows) for raw material, human resources and material are connected with the execution of each activity. Moreover, a large scaled project involves progress payments at previously determined time windows in order to guarantee a constant cash inflow and to secure the heavy cash outflows during the execution of the project. The complex interaction between these two cash flows leads to interesting insights during the scheduling of the project.
When one takes these financial aspects into account, the objective should be to maximize the net present value (npv) of the project. This well-known concept is based on a simple principle: accept the project when the npv > 0 and reject it when the npv < 0. The value of each cash flow (either inflow or outflow) is compounded towards the beginning of the project by means of the discount rate α as follows:
npv = sumi { ci * e-α * fi }
where sumi {} is used to take the sum over all project activities, ci denotes the cash flow linked with the execution of activity i, fi the finishing time of activity i in the baseline schedule and n the total number of activities in the project.
Scheduling objective: maximize the net present value
Once the project has been accepted (i.e. npv > 0), the accept/reject principle can be translated into an as- soon-as-possible/as-late-as-possible mechanism. Indeed, during the project scheduling phase, all activities have to be scheduled in time such that no precedence relations and resource constraints are violated. Time was, and still is, an important objective to that purpose, but financial aspects must be incorporated too. This translation is straightforward and lies in the very heart of the net present value: cash inflows should be scheduled as soon as possible while cash outflows should be scheduled as late as possible. Despite this simple principle, the construction of such a resource profile is a complex task.
Solving resource conflicts results in activity shifts in time in order to schedule them at periods where resources are still available. The choice of which activities have to be shifted depends on the scheduling objective. In “What is my scheduling objective? Minimizing the project lead time”, it has been shown that shifting activities 5 and 6 results in a resource-feasible schedule with a minimal project duration (i.e. 24 time periods), as displayed in figure 2.
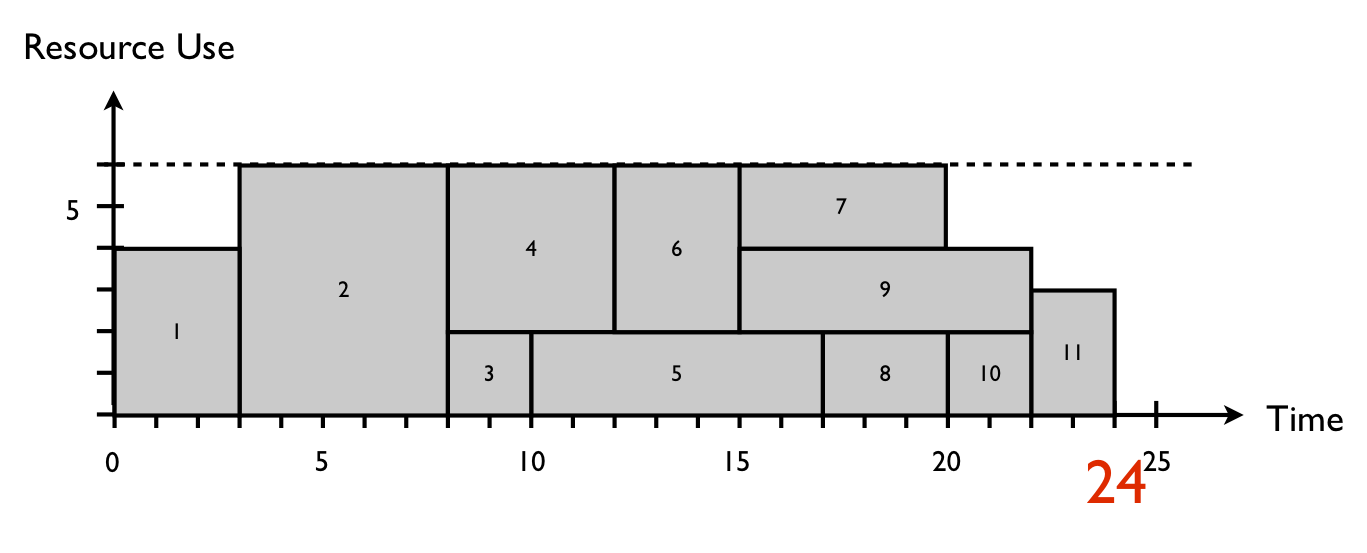
Figure 2: A resource-feasible project schedule with the lowest possible total project duration
However, a shift of activity 4 instead of 6 can result in a better schedule when the scheduling objective is to maximize the net present value. Indeed, activity 4 has a negative cash flow and needs to be scheduled as late as possible, while activity 6 has a positive cash flow, which gives the scheduler an incentive to schedule it as soon as possible. Although the minimization of the total project duration is not the scheduling objective, the presence of a big lump sum payment at the end of the project (activity 11) gives the scheduler the objective to finish the project as soon as possible, and hence, both time and npv are the scheduling objectives, resulting in the baseline schedule of figure 3.
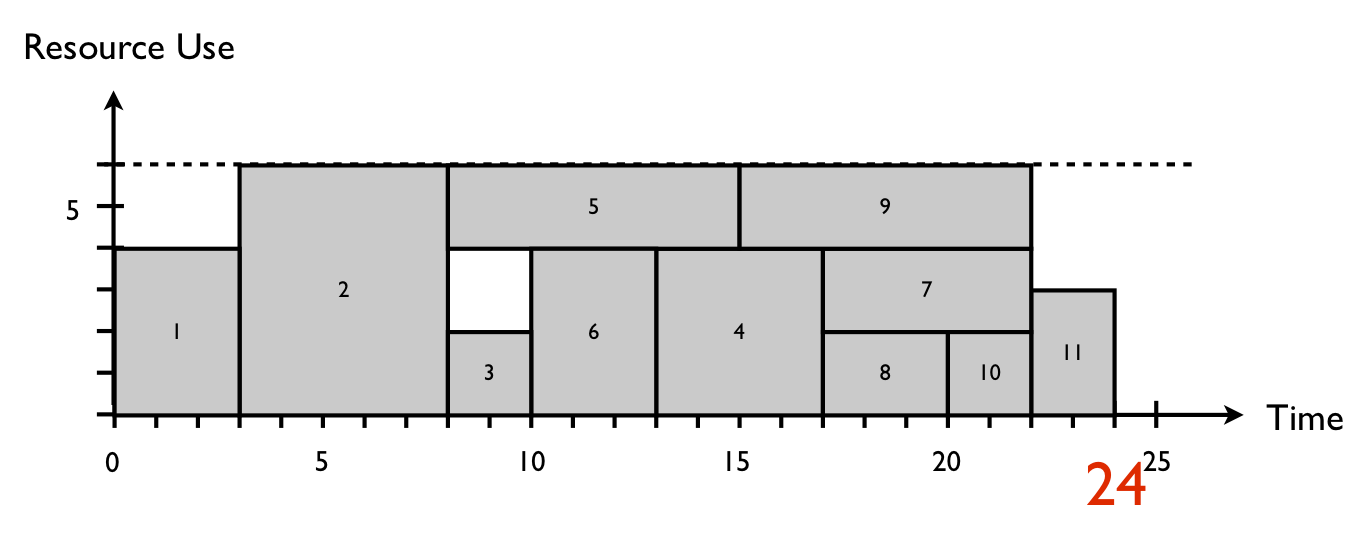
Figure 3: A resource-feasible project schedule with a maximum net present value
It is up to the reader to calculate the total net present value, which is equal to € 13.57 for the baseline schedule of figure 2 and € 15.23 for the schedule shown in figure 3, under the assumption that α = 5%. Note that the critical path in figure 1 is equal to the activity sequence 1 - 2 - 3 - 6 - 9 - 11 while the critical chain of figure 2 and figure 3 are equal to activity sequences 1 - 2 - 4 - 6 - 9 - 11 and 1 - 2 - 3 - 6 - 4 - 7 - 11, respectively. This example illustrates that the critical chain is not unique but depends on the scheduling objective and hence on the choice of delaying activities to solve resource conflicts (see “The critical path or the critical chain? The difference caused by resources”).
© OR-AS. PM Knowledge Center is made by OR-AS bvba | Contact us at info@or-as.be | Visit us at www.or-as.be | Follow us at @ORASTalks


