Scheduling a project without resources boils down to a sequencing problem where activities are iteratively scheduled while respecting the precedence relations between them. It results in the detection of the critical path which refers to a sub-part of the project network containing the activities that are critical to the project objective. In this article, the scheduling objective is assumed to be the minimization of the total project duration. Figure 1 displays a project network with 6 activities (A to F) and an activity duration estimate displayed above each node. This example will be used throughout this article to calculate the critical path.

Figure 1. An example project network
The determination of the critical path of a project requires three steps which are summarized along the following lines and discussed in the remainder of this article.:
-
Construct an earliest start schedule (ESS)
-
Construct a latest start schedule (LSS)
-
Calculate the activity slack
Earliest start schedule (ESS)
The earliest start of each activity can be calculated using forward calculations in the project network and is equal to the maximum of the earliest finishing times of all its predecessor activities. The earliest finish of an activity is defined as its earliest start time increased with its duration estimate. Figure 2 displays the ESS for the example project of figure 1, starting from the first activity A and working forwards to the last activity F, resulting in a total project duration of 15 time units.
Figure 2. An earliest start schedule for the example project
Latest start schedule (LSS)
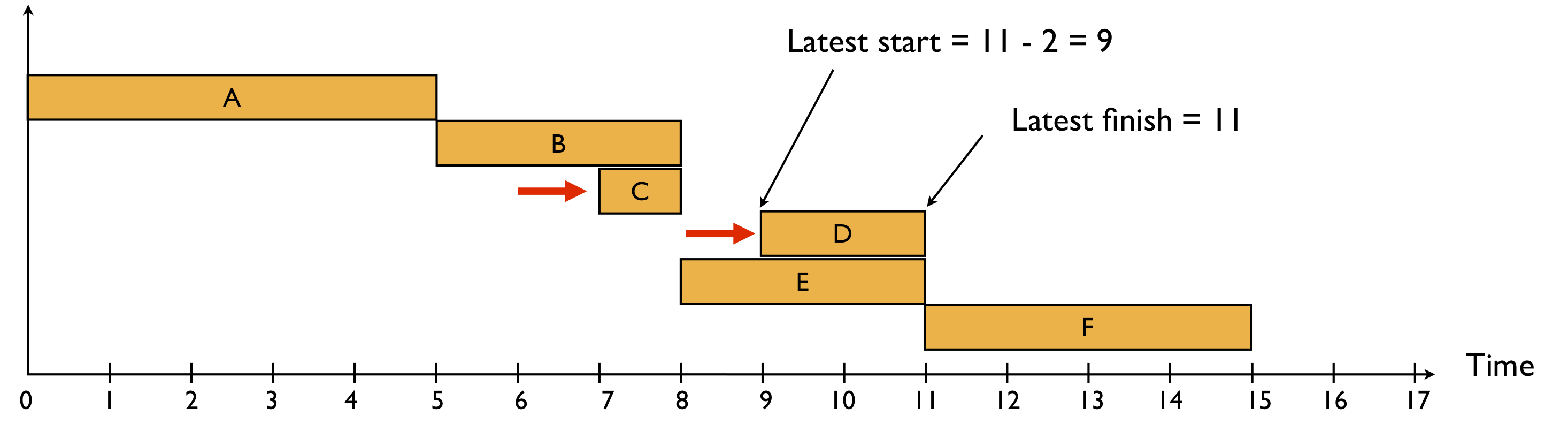
The latest finish of each activity can be calculated in an analogous way, using backward calculations, starting from the project deadline at the last activity of the project found by the ESS (which is equal to 15). It is equal to or or less than the latest start of all its successor activities. The latest start of an activity is defined as its latest finish time decreased by its duration estimate. Figure 3 displays the LSS, starting from the last activity F and working backwards to the first activity A, resulting in a total project duration of 15 time units.
Figure 3: A latest start schedule for the example project
Activity slack
The amount of slack (or float) associated with each activity is used to denote the free time of each activity within the ESS and LSS. It denotes the amount of time each activity can be delayed without violating the entire project duration. The slack of an activity can be calculated as the difference between its latest start and earliest start time, or alternatively, as the difference between its latest and earliest finishing time.
Activities with zero slack cannot be delayed without affecting the entire project duration and are called critical activities. The critical path consists of a path of critical activities and is given by activities A, B, E and F.
Activities that lie on the critical path cannot be delayed without delaying the entire project duration. Since time is an important objective in scheduling, the critical path is where the project manager has to focus on. It helps the manager to calculate the minimum length of time in which the project can be completed, and which activities should be prioritized to complete by that project deadline. In order to finish a project on time, the critical path calculations help the project manager to focus on the essential activities to which attention and resources should be devoted. It provides an effective basis for the scheduling and monitoring of project progress.