Resource constrained project scheduling: Regular and non-regular scheduling objectives
Submitted by Mario Vanhoucke on Fri, 12/30/2011 - 10:37
Project scheduling is the act of constructing a timetable for each project activity, respecting the precedence relations and the limited availability of the renewable resources, while optimizing a predefined scheduling objective (see “Resource constrained project scheduling: What is my scheduling objective?”). Although time is often considered as the dominant scheduling objective, other objectives are often crucial from a practical point-of-view. The various possible scheduling objectives can be classified in two categories, as follows:
- Regular scheduling objectives
- Non-regular scheduling objectives
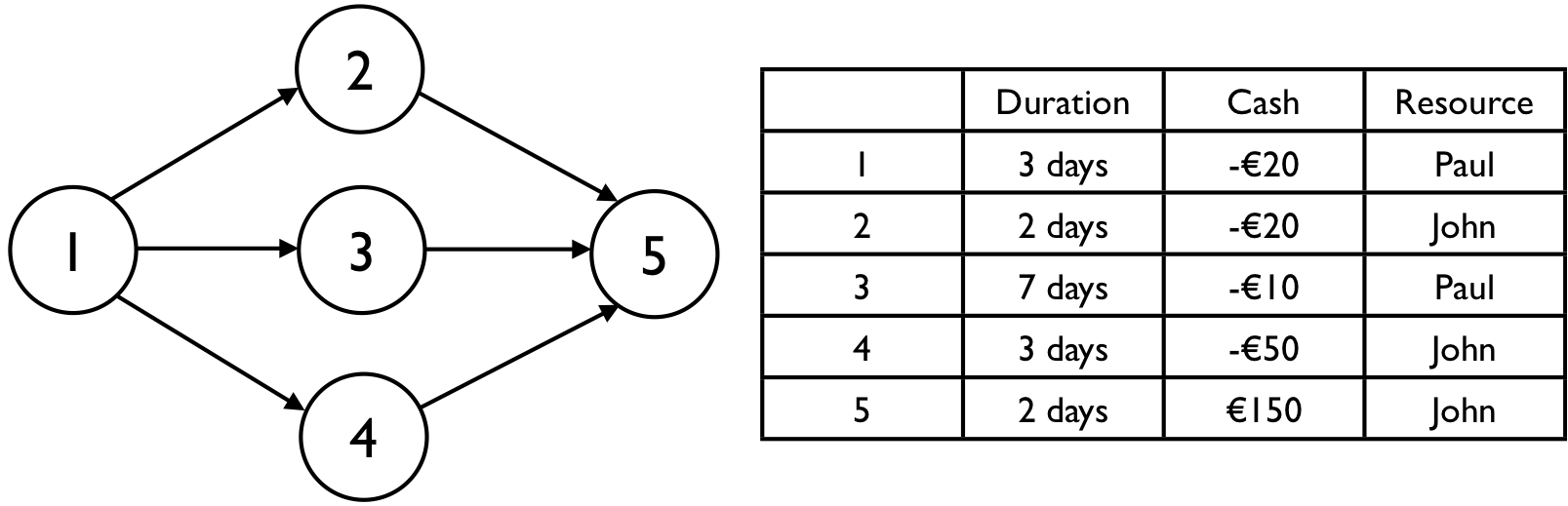
In this article, the difference between the two types of scheduling objectives is explained and illustrated on an example project shown in figure 1. The figure shows a project with 5 activities. Each project has a duration estimate, a cash flow (positive or negative) and a resource requirement as shown in the table to the right of the project network.

Figure 1. An example project network with activity durations, cash flows and resources
Regular scheduling objectives
Since the construction of a project schedule involves the presentation of an activity timetable, a schedule can be characterized by the starting time of the project activities. Assume two project schedules S and S’, each characterized by their activity starting times as follows:
- Schedule S: s1, s2, ..., sn
- Schedule S’: s’1, s’2, ..., s’n
with n the number of activities in the project.
A formal definition of a regular scheduling objective RSO can be given as follows:
Definition of regular scheduling objective
A regular scheduling objective RSO is a function of the activity starting times s1, s2, ..., sn such that
when
s1 ≤ s’1, s2 ≤ s’2,, ..., sn ≤ s’n
then
RSO(s1, s2, ..., sn) ≤ RSO(s’1, s’2, ..., s’n) for a minimization objective
or
RSO(s1, s2, ..., sn) ≥ RSO(s’1, s’2, ..., s’n) for a maximization objective
A non-regular scheduling objective is an objective for which this definition does not hold.
This definition implies that when two resource feasible schedules have been constructed such that each activity under the first schedule starts no later than the corresponding starting time in the second schedule, then the first schedule is at least as good as the second schedule. Consequently, it will never be beneficial to delay an activity of a resource feasible schedule towards the end of the project.
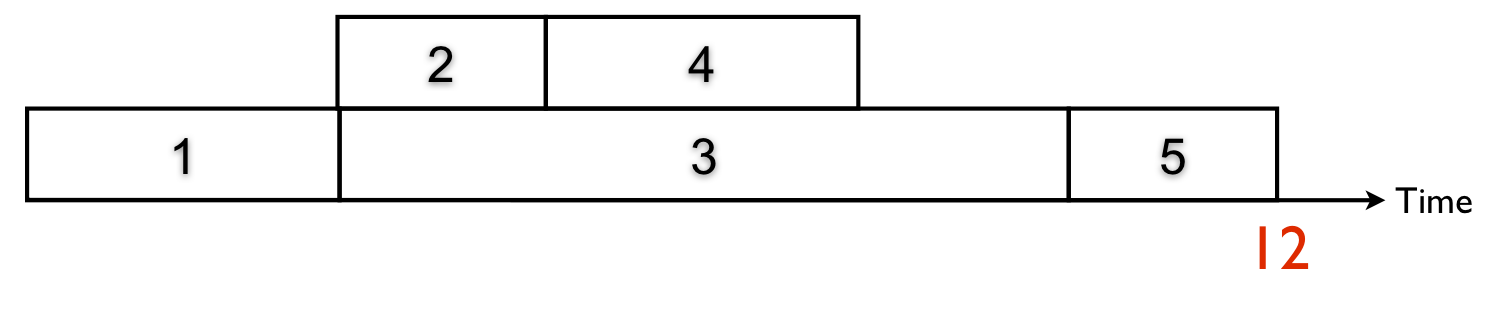
Figure 2 illustrates the definition on a project schedule with a time minimization scheduling objective. The schedule has a project deadline of 12 time units, and has no resource conflicts (see “The critical path or the critical chain? The difference caused by resources”). Minimizing the time of a project is a regular scheduling objective, and hence, it is never beneficial to delay an activity of a resource feasible schedule.
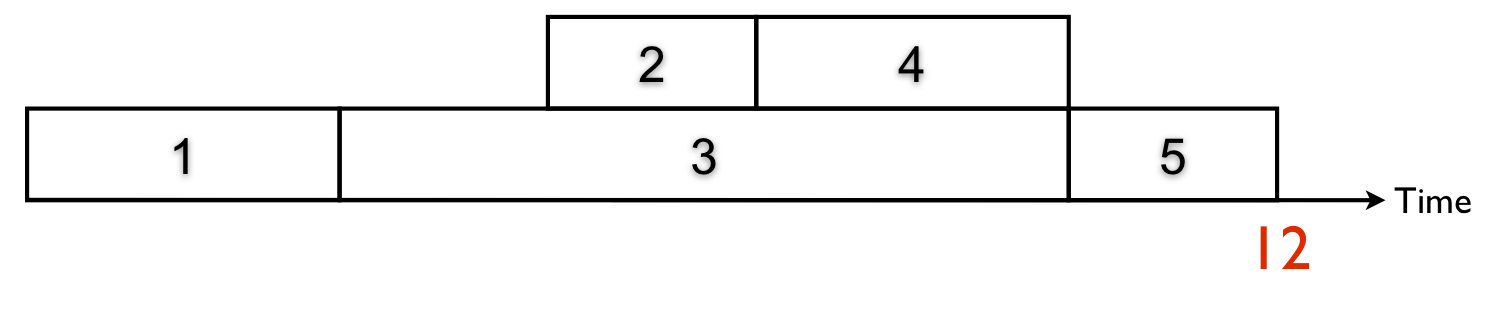
The definition of a regular scheduling objective can be illustrated on two project schedules shown in figures 2 and 3. The schedule S of figure 2 and the schedule S’ of figure 3 can be characterized by the following activity starting times:
- Schedule S: s1 = 0, s2 = 3, s3 = 3, s4 = 5, s5 = 10
- Schedule S’: s’1 = 0, s’2 = 5, s’3 = 3, s’4 = 7, s’5 = 10

Figure 2. An example schedule S for the network of figure 1

?Figure 3. An example schedule S’ for the network of figure 1
It is clear that all starting times of schedule S are lower than or equal to the starting times of schedule S’. Indeed, delaying activities 1, 3 or 5 would lead to an increase of the total project duration of 12. Delaying activities 2 and 4 would not lead to a project duration increase when they are delayed within their slack. Consequently, delaying activities in the schedule of figure 2 will never lead to an improvement of the scheduling objective, i.e. in a project duration reduction. This corresponds to the formal definition, i.e. TIME(s1 = 0, s2 = 3, s3 = 3, s4 = 5, s5 = 10) = 12 ≤ TIME(s’1 = 0, s’2 = 5, s’3 = 3, s’4 = 7, s’5 = 10) = 12.
Constructing resource feasible project schedules with regular scheduling objectives can be done by using priority rules and generation schemes, as discussed in “Optimizing regular scheduling objectives: Priority rule based scheduling”.
Non-regular scheduling objectives
A non-regular scheduling objective is an objective for which the formal definition above does not hold. Consequently, a given resource feasible schedule can be improved by delaying one or more activities towards the end. A typical non-regular scheduling objective is the maximization of the net present value of a project, where activities with positive cash flows are scheduled as-soon-as-possible, while activities with negative cash flows are scheduled as-late-as-possible (see “What is my scheduling objective? Maximizing the net present value”).
In the example project schedules of figures 2 and 3, it is clear that delaying activities 2 and 4 of schedule S leads to an improvement of the scheduling objective, since it increases the net present value. Consequently, the schedule S’ has a higher net present value than the schedule S, and hence, the definition above does not hold, i.e. NPV(s1 = 0, s2 = 3, s3 = 3, s4 = 5, s5 = 10) is not larger than or equal to NPV(s’1 = 0, s’2 = 5, s’3 = 3, s’4 = 7, s’5 = 10).
Other non-regular scheduling objectives are the idle time minimization and the resource leveling objective, as discussed in “What is my scheduling objective? Minimizing the resource idle time” and “What is my scheduling objective? Leveling the use of resources”.
Constructing resource feasible project schedules with non-regular scheduling objectives can be done by using priority rules and an iterative shifting algorithm, such as the Burgess and Killebrew algorithm, which will not be discussed at PM Knowledge Center.
© OR-AS. PM Knowledge Center is made by OR-AS bvba | Contact us at info@or-as.be | Visit us at www.or-as.be | Follow us at @ORASTalks


