A project network consists of a set of activities, represented as nodes in a network between which links are drawn to represent the technological precedence relations between these project activities (see “Activity links: How to add precedence relations between activities?”).
These precedence relations can be one out of four types (start-start (SS), start-finish (SF), finish-start (FS) and finish-finish (FF)), with a positive, zero or negative time-lag to express a minimal or a maximal time window between two activities.
In figure 1, a finish-start precedence relation between activities 1 and 2 with a minimal time-lag of 3 days is used to imply that activity 2 can not start earlier than three days after the finish of activity 1.
Figure 1: An example activity link between activity 1 and 2
In this article, it will be shown that each of the four types of precedence relations can be transformed to any other type, and that the equivalence between minimal and maximal time-lags can be easily shown by adding reverse arcs in a project network, as given along the following lines:
-
SS, SF and FF to FS transformations
-
Maximal to minimal transformations
Minimal time-lag transformations
Each precedence relation has a time-lag to denote a minimal time-span between the two activities. Time-lags can be positive, zero or negative, and can be used in combination with each of the four precedence relation types. Figure 2 shows the four types of relations between activities 1 and 2, where the width of the bar represents the duration of both activities.
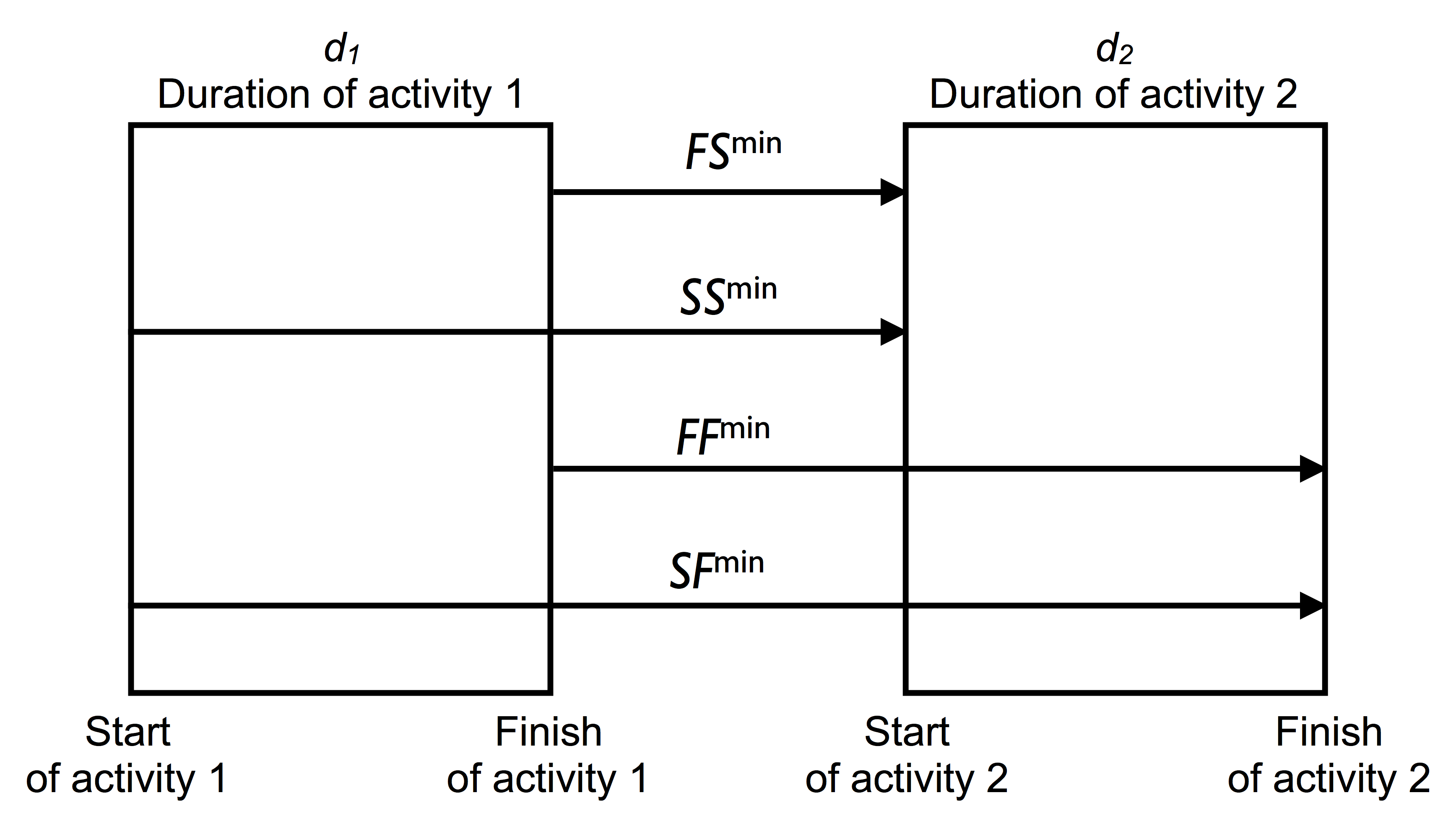 Figure 2: Four different types of minimal precedence relations
Figure 2: Four different types of minimal precedence relations
Since a finish-start (FS) relation can be considered as the default precedence relation, figure 2 will be used to illustrate the transformation of a SS, SF and FF relation to a FS relation, using the following simple formulas:
-
SS = FS + d1
-
FS = FS
-
SF = FS + d1 + d2
-
FF = FS + d2
with dx the duration of activity x.
As an example, a finish-start relation between two activities, with durations equal to 5 and 7 for activities 1 and 2, respectively, and a minimal time-lag of 4 days is identical to a start-start relation with a time-lag of 9 days, a start-finish relation with a time-lag of 16 days and a finish-finish relation with a time-lag of 11 days.
Minimal and maximal time-lag equivalence
The minimal time-lag transformations discussed previously can be extended to maximal time-lags, where similar equations can be used. Moreover, the equivalence between minimal and maximal time-lags can be easily obtained by reversing project network arcs. Indeed, a maximal time-lag can be represented by a negative minimal time-lag with an arc between the two activities in the opposite direction. Consequently, project networks with generalized precedence relations can be represented by cyclic networks, which often lead to an increased complexity or which are sometimes completely unacceptable in project management software tools.Figure 3 shows such a transformation from a maximal finish-start relation (FSmax = 3) between activities 1 and 2 to a minimal start-finish relation (SFmin = −3) between activities 2 and 1. Activity 2 is allowed to start maximum 3 time periods after the finish of activity 1, which is exactly the same as specifying that activity 1 can only finish minimum -3 time periods after the start of activity 2.
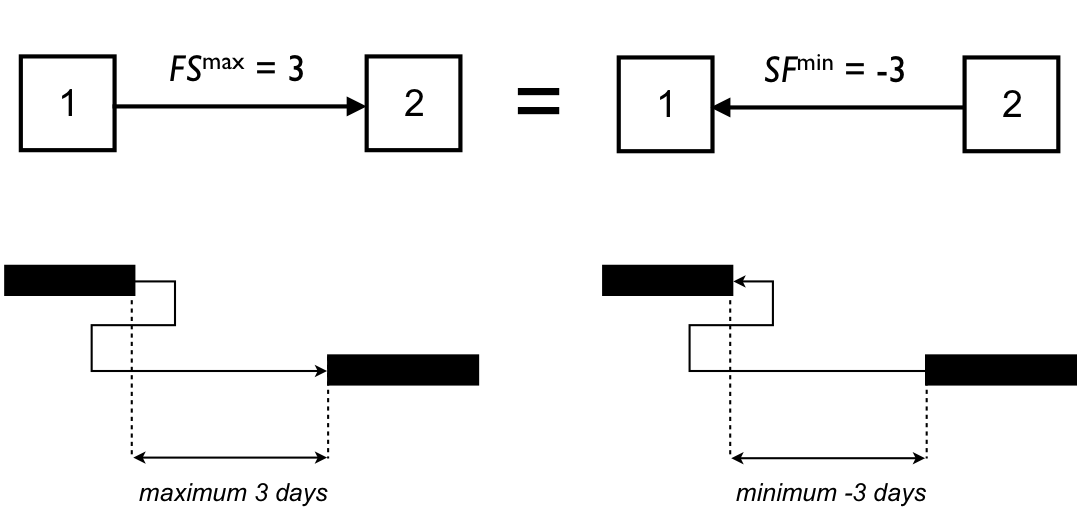
Figure 3: The equivalence of minimal and maximal time lags
Obviously, this equivalence also holds for the other three types (SS, SF and FF).
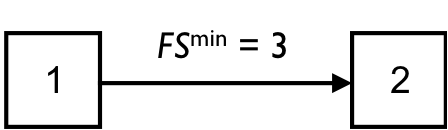
 Figure 2: Four different types of minimal precedence relations
Figure 2: Four different types of minimal precedence relations



